- To factor a number M, we choose a number y < M with
gcd(y,M) = 1. We then find r, the order of y in the multiplicative group
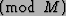 .
If r is even, then
(yr/2+1)(yr/2-1)=
.
If r is even, then
(yr/2+1)(yr/2-1)=
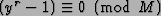 .
Then
gcd(yr-1,M) is a non-trivial factor of M except when r is odd or
.
Then
gcd(yr-1,M) is a non-trivial factor of M except when r is odd or
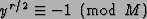 .
This procedure produces a non-trivial factor of M with probability at least
1 - 1/2k-1, where k is the number of distinct odd prime factors of M. If we don't get a factor, we can choose a new y and repeat the process. By repeating the process, we can make our likelihood of success as close to one as we like. Note that if M is even, finding a factor is easy; if M is a power of a prime, there are other fast classical methods of factoring which we can use on M before we start this process.
.
This procedure produces a non-trivial factor of M with probability at least
1 - 1/2k-1, where k is the number of distinct odd prime factors of M. If we don't get a factor, we can choose a new y and repeat the process. By repeating the process, we can make our likelihood of success as close to one as we like. Note that if M is even, finding a factor is easy; if M is a power of a prime, there are other fast classical methods of factoring which we can use on M before we start this process.
- We want to find the period of the function
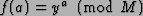 .
We do that by measuring to find a state whose amplitude has the same period as f.
.
We do that by measuring to find a state whose amplitude has the same period as f.
We measure the qubits of the state obtained from encoding f(a).
A random value u is obtained. We don't actually use the
value u; only the
effect the measurement has on our set of superpositions is of interest.
This measurement projects the state space onto the
subspace compatible with the measured value, so the state after
measurement is
for some scale factor C where
Note that the a's that actually appear in the sum, those with 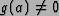 ,
differ from each other by multiples of the period, and thus g(a) is the
function we are looking for. If we could just measure
two successive a's in the sum, we would have the period.
Unfortunately the quantum world permits only one measurement.
,
differ from each other by multiples of the period, and thus g(a) is the
function we are looking for. If we could just measure
two successive a's in the sum, we would have the period.
Unfortunately the quantum world permits only one measurement.
- Shor's method uses a quantum version of the Fourier transform to find the period of the function
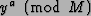 .
We apply the quantum Fourier transform to the state obtained by the measurement.
.
We apply the quantum Fourier transform to the state obtained by the measurement.
Standard Fourier analysis tells us that when the
period r of g(a) is a power of two, the result of the quantum Fourier
transform is
where
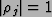 .
When the period r does not divide 2n, the transform approximates
the exact case so most of the amplitude
is attached to integers close to multiples of
.
When the period r does not divide 2n, the transform approximates
the exact case so most of the amplitude
is attached to integers close to multiples of
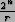 .
.
- In order for Shor's factoring algorithm to be a polynomial algorithm, the quantum
Fourier transform must be efficiently computable. Shor
developed a quantum Fourier transform construction with base 2n using
only
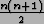 gates. The construction makes use of two types of
gates. One is a gate to perform the Hadamard transformation H.
We will denote by Hj the Hadamard transformation applied to the jth
bit. The other type of gate performs transformations of the form
gates. The construction makes use of two types of
gates. One is a gate to perform the Hadamard transformation H.
We will denote by Hj the Hadamard transformation applied to the jth
bit. The other type of gate performs transformations of the form
where
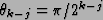 ,
which acts on the kth element,
depending on the value of the jth element. Think of this as acting on the basis
,
which acts on the kth element,
depending on the value of the jth element. Think of this as acting on the basis
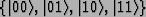 ...
...
The quantum Fourier transform is given by
Hn-3Sn-3,n-2Sn-3,n-1Hn-2Sn-2,n-1Hn-1.
This actually produces the reverse of the Fourier transform, so it typically will be followed by a bit reversal transformation.
- There is a second piece of Shor's algorithm which must be accomplished in polynomial time. We need to extract (using the QFT) the period of the function
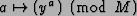 .
We must transform as:
.
We must transform as:
We want to develop a transformation which computes the function
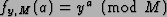 .
First,
we write ya as
.
First,
we write ya as
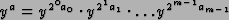 ,
where m is the number of digits in the binary expansion of M. Then, modular exponentiation can be
computed by initializing the result register to
,
where m is the number of digits in the binary expansion of M. Then, modular exponentiation can be
computed by initializing the result register to
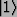 ,
and
successively effecting m multiplications by
,
and
successively effecting m multiplications by
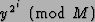 ,
depending on the value of the qubit
,
depending on the value of the qubit
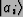 .
If ai=1, we want
the operation
.
If ai=1, we want
the operation
to be performed; otherwise, when
ai=0 we just require
Note that in both cases the result can be written as
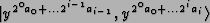 .
.
- To extract the period, we measure the state in the standard basis for quantum computation,
and call the result v. In the case
where the period happens to be a power of 2 so that
the quantum Fourier transform gives exactly multiples of the scaled
frequency, the period is easy to extract. In this case,
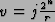 for some j. Most of the time j and r will
be relatively prime, in which case reducing the fraction
for some j. Most of the time j and r will
be relatively prime, in which case reducing the fraction
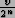 to its lowest terms will yield a fraction whose denominator qis the period r. The fact that in general the quantum Fourier
transform only gives approximately multiples of the scaled
frequency complicates the extraction of the period from the
measurement. When the period is not a power of 2, a good guess for
the period can be obtained using the continued fraction expansion of
to its lowest terms will yield a fraction whose denominator qis the period r. The fact that in general the quantum Fourier
transform only gives approximately multiples of the scaled
frequency complicates the extraction of the period from the
measurement. When the period is not a power of 2, a good guess for
the period can be obtained using the continued fraction expansion of
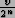 .
.
- Various things could have gone wrong so that this process does
not yield a factor of M:
- 1.
- The value v was not close enough to a multiple of
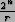 .
.
- 2.
- The period r and the multiplier j could have had a common factor
so that the denominator q was actually a factor of the period, rather than the
period itself.
- 3.
- We find M as M's factor.
- 4.
- The period of
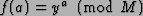 is odd.
is odd.
A few repetitions of this algorithm yields a factor of M with
high probability.
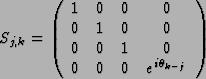
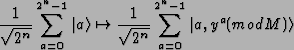
![]() .
First,
we write ya as
.
First,
we write ya as
![]() ,
where m is the number of digits in the binary expansion of M. Then, modular exponentiation can be
computed by initializing the result register to
,
where m is the number of digits in the binary expansion of M. Then, modular exponentiation can be
computed by initializing the result register to
![]() ,
and
successively effecting m multiplications by
,
and
successively effecting m multiplications by
![]() ,
depending on the value of the qubit
,
depending on the value of the qubit
![]() .
If ai=1, we want
the operation
.
If ai=1, we want
the operation
 .
.
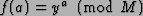 is odd.
is odd.