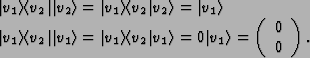Next: Tensor products
Up: A brief overview of
Previous: Our general topics:
- A Hilbert space
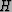 is a complete normed vector space over
is a complete normed vector space over
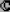 :
:
- 1.
-
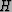 is a vector space over
is a vector space over
- 2.
- There is an inner product
 :
:
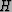 x
x

which is conjugate linear:
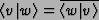
 for
for

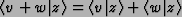
 and
and
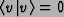 iff v = 0
iff v = 0 - 3.
- From the inner product, as usual, we define the norm of a vector:
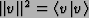
- 4.
-
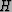 is complete with respect to the norm.
is complete with respect to the norm.
- We will typically use the bra/ket notation:
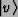 is a vector in
is a vector in
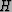 ,
and
,
and
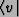 is the covector which is the conjugate transpose of v.
is the covector which is the conjugate transpose of v.
- This notation also allows us to represent the outer product of a vector and
covector as
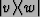 ,
which, for example, acts on a vector
,
which, for example, acts on a vector
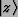 as
as
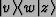 .
For example, if {v1,v2} is an orthonormal basis for a two-dimensional
Hilbert space,
.
For example, if {v1,v2} is an orthonormal basis for a two-dimensional
Hilbert space,
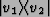 is the transformation
that maps
is the transformation
that maps
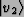 to
to
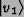 and
and
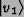 to (0, 0)T since
to (0, 0)T since
Equivalently,
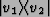 can be written in matrix form where
can be written in matrix form where
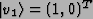 ,
,
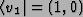 ,
,
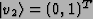 ,
and
,
and
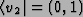 .
Then
.
Then
- A unitary operator
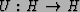 is a linear mapping
whose conjugate transpose is its inverse:
is a linear mapping
whose conjugate transpose is its inverse:
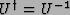
- Unitary operators are norm preserving:
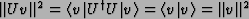
- We will think of a quantum state as a (normalized) vector
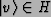 .
For math folks, we are in effect working in Complex projective space, normalizing
to 1 so that the probabilities make sense.
.
For math folks, we are in effect working in Complex projective space, normalizing
to 1 so that the probabilities make sense.
- The dynamical evolution of a quantum system is expressed as a unitary operator acting on
the quantum state.
- Eigenvalues of a unitary matrix are of the form
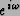 where
where 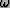 is a
real-valued angle. A unitary operator is in effect a rotation.
is a
real-valued angle. A unitary operator is in effect a rotation.
- Just for reference, a typical expression of Schrödinger's equation looks like
with general solution
where
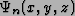 is an eigenfunction solution of the time independent Schrödinger
equation with En the corresponding eigenvalue. The inner product, giving a time
dependent probability, looks like
is an eigenfunction solution of the time independent Schrödinger
equation with En the corresponding eigenvalue. The inner product, giving a time
dependent probability, looks like
- Another way to think of this is that we have to find the Hamiltonian
 which generates evolution according to:
which generates evolution according to:
In our context, we will have to solve for  given a desired U:
given a desired U:
A solution for  always exists,
as long as the linear operator U is unitary.
always exists,
as long as the linear operator U is unitary.
- A measurement consists of applying an operator O to a quantum state v. To
correspond to a classical observable, O must be Hermitian,
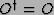 ,
so
that all its eigenvalues are real. If one of its eigenvalues
,
so
that all its eigenvalues are real. If one of its eigenvalues 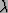 is associated with
a single eigenvector
is associated with
a single eigenvector 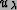 ,
then we observe the value
,
then we observe the value 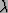 with probability
with probability
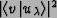 (i.e., the square of the length of
the projection along
(i.e., the square of the length of
the projection along 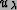 ).
).



Next: Tensor products
Up: A brief overview of
Previous: Our general topics:
Tom Carter
1999-05-17
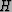 is a vector space over
is a vector space over
 :
:
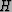 x
x

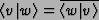
 for
for

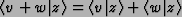
 and
and
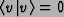 iff v = 0
iff v = 0 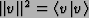
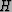 is complete with respect to the norm.
is complete with respect to the norm.